 |
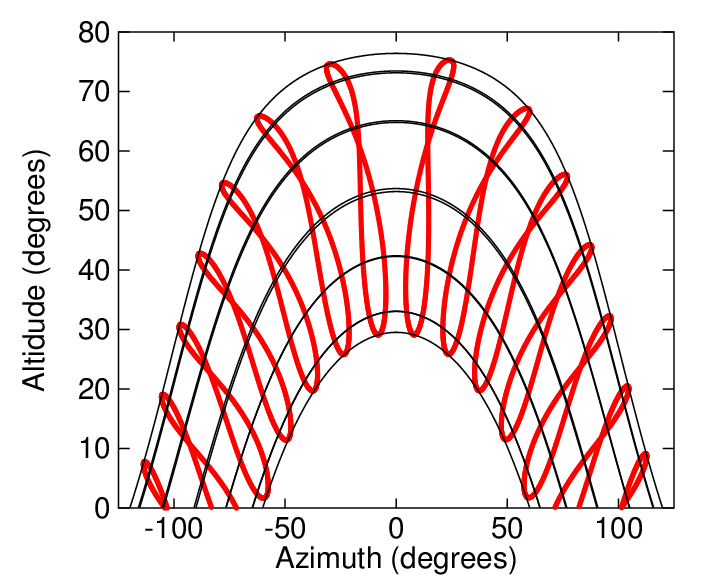
analemma.m position of sun in sky |
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Octave (Matlab) script to calculate position of sun in the sky %
% Peter Stallinga, February 2012 %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all;
hold off;
clc; home;
% Part I: Inspired by http://www.stargazing.net/kepler/sun.html
%1. Find the days before J2000.0 (d) from the table
function [azi,alti] = azialti(y, m, d, h, mins, north, east)
h = h+mins/60.0;
%1. Find the day:
d = 367 * y - floor(7 * (y +floor( (m + 9)/12))/ 4) + floor(275 * m / 9) + d - 730531.5 + h / 24;
%2. Find the Mean Longitude (L) of the Sun
%L = fmod(280.461 + 0.9856474 * d, 360.0);
L = 280.461 + 0.9856474 * d;
while (L<0)
L = L+360.0;
endwhile
%3. Find the Mean anomaly (g) of the Sun
g = 357.528 + 0.9856003 * d;
%4. Find the ecliptic longitude (lambda) of the sun
lambda = L + 1.915 * sin(g*pi/180.0) + 0.020 * sin(2*g*pi/180.0);
% (note that the sin(g) and sin(2*g) terms constitute an
% approximation to the 'equation of centre' for the orbit
% of the Sun)
% beta = 0;
% (by definition as the Sun's orbit defines the
% ecliptic plane. This results in a simplification
% of the formulas below)
%5. Find the obliquity of the ecliptic plane (epsilon)
epsilon = 23.439 - 0.0000004 * d;
%6. Find the Right Ascension (alpha) and Declination (delta) of the Sun
Y = cos(epsilon*pi/180.0) * sin(lambda*pi/180.0);
X = cos(lambda*pi/180.0);
a = (180.0/pi)*atan(Y/X);
if (X < 0)
alpha = a + 180;
else
if (Y < 0) && (X > 0)
alpha = a + 360;
else
alpha = a;
endif
endif
alpha;
delta = (180.0/pi)*asin(sin(epsilon*pi/180.0)*sin(lambda*pi/180.0));
% Part II: From http://www.geoastro.de/elevaz/basics/index.htm
%compute Sidereal time at Greenwich:
T = d/ 36525.0;
theta0 = 280.46061837 + 360.98564736629*d + 0.000387933*T*T - T*T*T/38710000.0;
while (theta0<0)
theta0 = theta0+360.0;
endwhile
theta0;
theta = theta0 + east;
tau = theta - alpha;
beta = north;
beta = pi*beta/180.0;
delta = pi*delta/180.0;
tau = pi*tau/180.0;
alt = asin(sin(beta)*sin(delta) + cos(beta)*cos(delta)*cos(tau));
az = atan2(- sin(tau) , (cos(beta)*tan(delta) - sin(beta)*cos(tau)));
alti = 180.0*alt/pi;
azi = 180.0*az/pi-180.0;
if azi<-180.0
azi=azi+360.0;
endif
if azi>180.0
azi=azi-360.0;
endif
endfunction
maanden = [31,28,31,30,31,30,31,31,30,31,30,31]; % months
y = 2011.0;
% Position of: Faro Vale da Amoreira
north = 37.028176;
east = -7.931132;
% part 1: analemmas:
for h=1:23
i = 0;
for n=1:365
d = n;
m = 1;
while (d>maanden(m))
d = d - maanden(m);
m = m+1;
endwhile
[az, alt] = azialti(y, m, d, h, 0, north, east);
%if ((alt>0) && (az<-30.0))
if (alt>0)
i=i+1;
az0h(h, i)=az;
alt0h(h, i)=alt;
endif
endfor
aserieslen(h)=i;
endfor
% part 2. Trajectory on day 21 of each month:
for m=1:12
n=0;
d = 21;
h=23.00;
mins=0;
alt = 100;
while (h>0)
[az,alt] = azialti(y, m, d, h, mins, north, east);
%if ((alt>0) && (az<-30.0))
if (alt>0)
n=n+1;
az21m(m,n)=az;
alt21m(m,n)=alt;
endif
mins=mins-1;
if (mins<0)
mins=mins+60;
h = h-1;
endif
endwhile
bserieslen(m)=n;
endfor
hold off;
for h=1:23
if aserieslen(h)>0
plot(az0h(h,1:aserieslen(h)), alt0h(h,1:aserieslen(h)),'bo');
hold on;
endif
endfor
for m=1:12
if bserieslen(m)>0
plot(az21m(m,1:bserieslen(m)), alt21m(m,1:bserieslen(m)),'k-');
endif
endfor
xlabel('Azimuth (degrees)');
ylabel('Altitude (degrees)');
axis('tight');
title('Position of Sun 2011. 0^o is South, -90^o is East, +90^o is West');
For more information, contact me at The University of The Algarve,
Prof. Peter Stallinga
http://www.stallinga.org