Theory of Metal-Insulator-Semiconductor Field-Effect Transistors (MOS-FET)

When I wrote this in 2004, I tried to make theory pages for our research on organic thin-film transistors (TFTs). At that time, I did, just like everybody else, make the assumption that a thin-film transistor is just like a thin MOS-FET. Any theory of a MOS-FET I assumed to be directly applicable to a TFT. This, however, proved to be wrong. Recently we developed a theory specially designed for thin-film transistors (organic and inorganic alike). Click here (http://www.ualg.pt/fct/adeec/optoel/theory/tft/) if you want to study TFT instead of MOS-FETs. These pages now exclusively deal with MOS-FETs. At this moment, these pages are no longer relevant to our research, but I keep them because they might anyway be interesting for some people.
(in case you already want to see the TFT model, look for the two publications in Synthetic Metals 156, p.1305 and p.1316).

The idea is here to present the theory of metal-insulator-semiconductor field-effect transistors. I will try to do this in a very simplified way, cutting away all the details. However, I am well aware that in this way, I may oversimplify things. This should serve as an introduction to get a feeling for electronic devices. This guide does not substitute serious books like Sze and Shur, whose reference can be found at the end of this document.

As we will see, the MIS-FET can be well described by a MIS-diode with source and drain electrodes connected in the plain of the active layer. Therefore, it is best to start with the MIS junction.

::: MIS junction.
::: Capacitance of an MIS junction
::: Field-Effect transistor (inversion channel)
             -- Linear region
             -- Threshold voltage of an inversion-channel FET
             -- Subthreshold region of an inversion-channel FET
             -- Saturation
             -- Short-channel effects

Peter Stallinga, July 2007.

MIS junction

To understand how an FET (of the MOSFET type) works, we first have to analyze what an MIS structure is.
In a simple approximation, a MOSFET is a planar device of semiconducting material whose free carrier concentration n, and hence it conductivity (via g = m_en) is controlled by the gate.

The first figure shows an energy diagram of an MIS device. The device consists of a metal and a semiconductor separated by an insulator. Here we assume that the insulator is not conducting any current.
Standard textbooks start with an ideal MIS device, which means that the Fermi levels in the metal and the semiconductor are aligned even before contact. In other words, the work functions of the metal and of the semiconductor are equal, f_m = c + E_C-E_F. This implies that we have no band bending in the absence of external voltages. Remember the Schottky barrier, where charge was flowing from one side to the other due to the misalignment of the Fermi levels. In the ideal MIS junction such a flow of charge is not needed (which saves us the trouble of explaining how it can pass through the oxide :-)

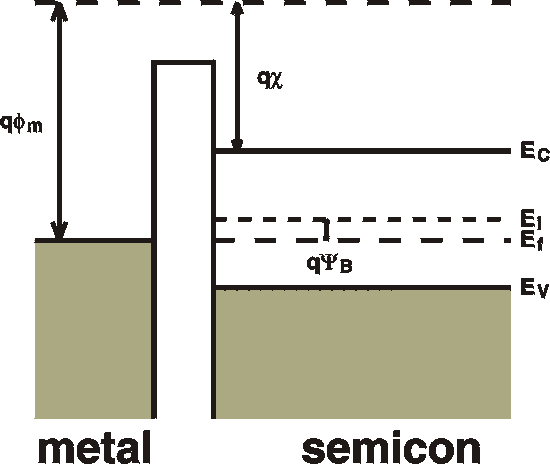MIS f_m : the metal workfunction. How much it costs to take an electron from the top of the sea of electrons in the metal to vacuum. The "workfunction" of the semiconductor can be defined as c + E_C-E_F.
f_b : (not shown, because it doesn't enter into the calculations): the barrier height of the oxide as seen from the metal; the difference between the "conduction band" of the oxide and the Fermi level of the metal..
c : the electron affinity of the semiconductor. The energy it takes to take an electron from the conduction band to the vacuum level.
E_G : energy gap of the semiconductor.
Y_B : the energy from the midgap level to the Fermi level. This is approximately equal to E_G/2
E_C : bottom of conduction band.
E_V : top of valence band.

The following strip explains what happens when we connect an external voltage to the metal (gate). For that we use the legend as shown here on the right.
Note that the (horizontal) SCALE of the pictures is changing. Just like in Schottky barriers, the depletion width depends on the voltage. Here the depletion width is shown as constant.
Legend

a) Depletion
MIS depletion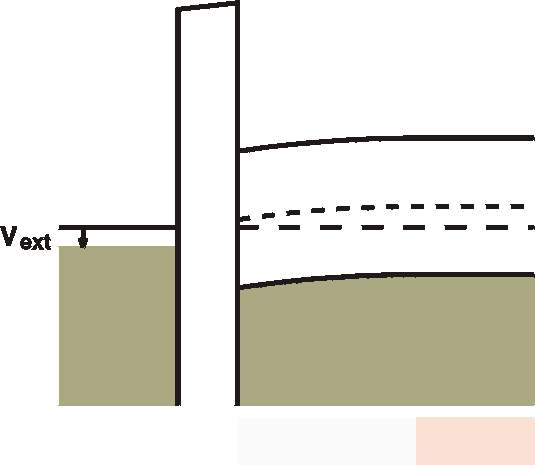
When a small (positive) voltage is connected to the metal (gate), free holes are pushed out of the interface region and a band bending results on the other side of the insulator. This is the same effect as seen in a Schottky barrier. Free carriers (holes) flow out of the interface region and a depletion zone is formed. The uncompensated (negatively) ionized acceptors cause an electric field and - via Poisson's equation - a parabolic bending of the bands.
Note that there is also a voltage drop in the oxide. In the oxide no charges can reside and hence the field is constant and the voltage drop is linear in space. The total voltage drop in the oxide plus the band bending is equal to the external voltage.

b) Inversion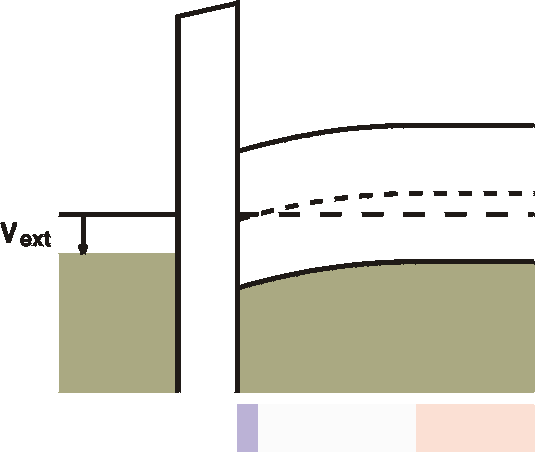
MIS inversion
When the voltage is further increased, at the interface an inversion region is created. The semiconductor becomes here n-type, albeit not very conductive, yet.

c) Strong Inversion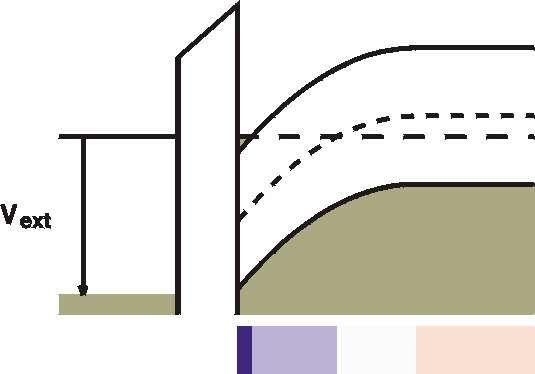
MIS strong inversion
For very strong bias, the Fermi level crosses the conduction band close to the interface. This is strong inversion. Free electrons are in a so-called "channel" next to the oxide. This channel is therefore highly conductive.
The ample availability of states in the conduction band means that further increases in the gate voltage will not extend this strong inversion region into space, but rather will increase the density of electrons in the channels. The channel is always infinitesimally thin.The huge amounts of free carriers can easily cause a large voltage drop (band bending) and only a thin layer is needed to "absorb" the external voltage.
Note that the depletion width (the white zone) and the inversion width (light blue zone) are constant once the channel is formed.

d) Accumulation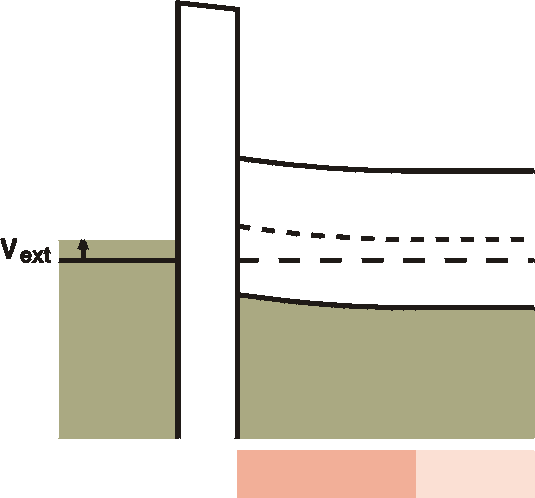
MIS accumulation
Going in the other direction, a negative voltage at the gate metal will attract some free holes to the interface. In this accumulation region, an increased number of free holes is created, although it is not yet dramatic; the interface is still high-ohmic.

e) Strong accumulation
MIS strong accumulation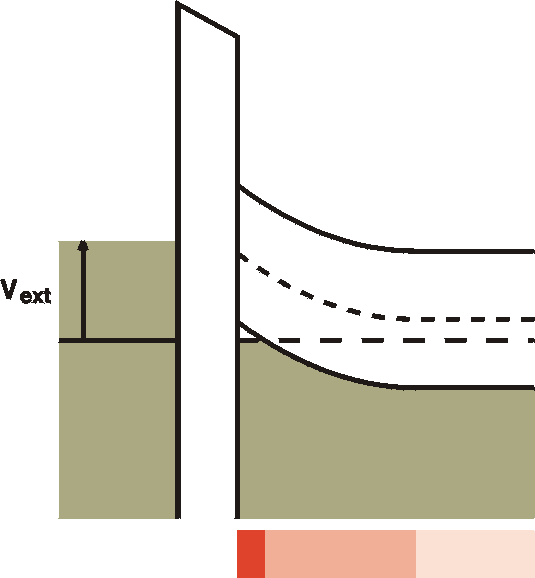
For stronger negative voltages at the gate the Fermi level is forced below the valence band at the interface. A channel with high density free holes is created. This is called strong accummulation.
Again, as for the strong inversion case, further increasing the voltage will result in an increase of the density of the free holes rather than an increase of the channel in space. In the picture the width of the channel is exaggerated. In reality it is only a monolayer thick.

To complete the story, in strong inversion we have the following distribution of space charge and free carriers:

The MIS junction is an ideal device for studying interface states and deep levels using the same techniques as demonstrated for the Schottky barrier. The advantage lies in the fact that there is no DC current which might obscure our measurements.

Capacitance of an MIS junction:

The device can consist of several regions in series, each with it's own capcitance. The capacitance of the metal and of any part of the semiconductor with free carriers is zero. For the other two parts of the device, the insulator and the depletion region we can calculate:
C_ox = e_ox/ d
C_W = e_s/ W
The total capacitance is caluclated by taking the serial sum of the capacitances:

	C_ox x C_W
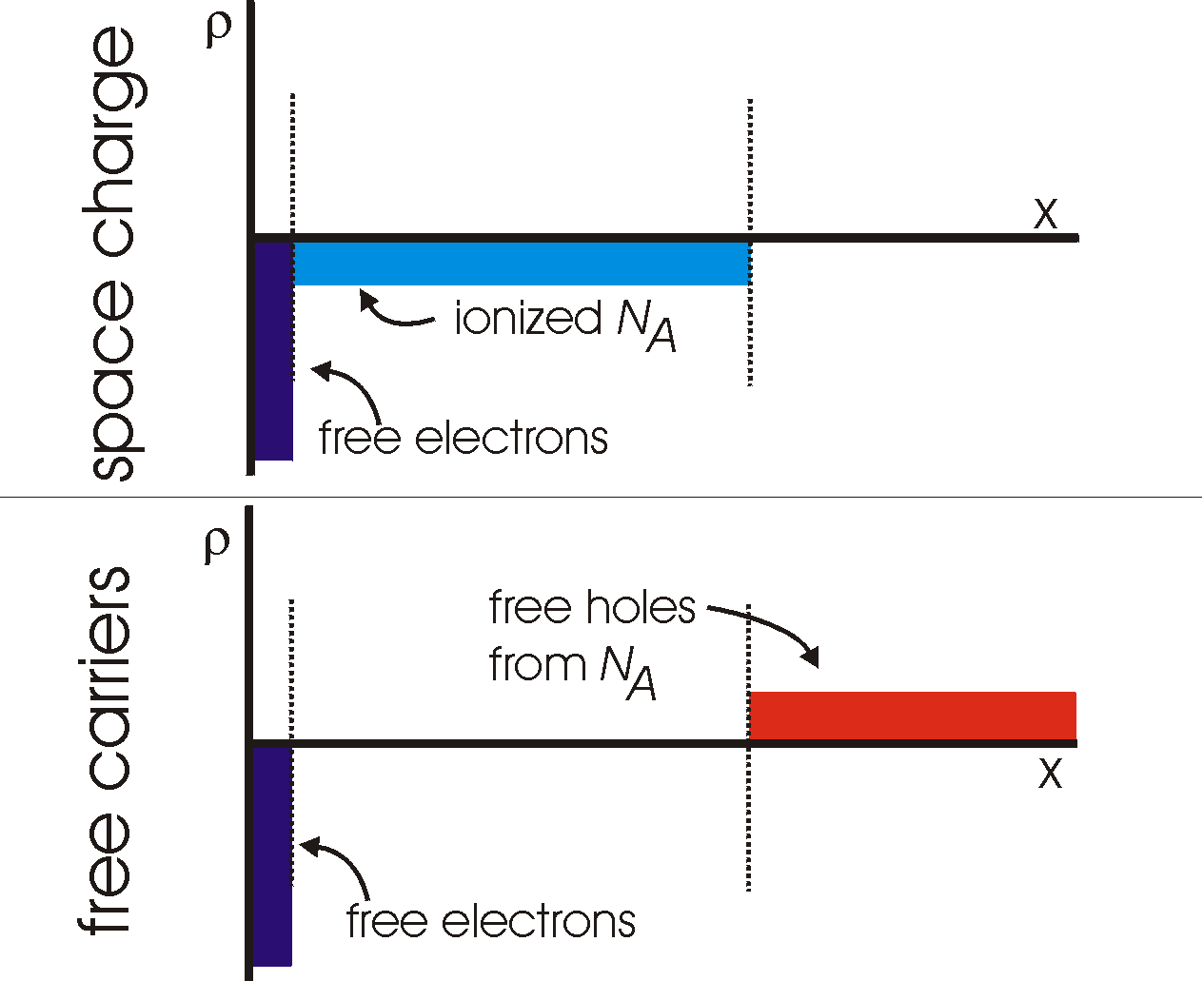
depletion: C_d =	-----------	accumulation: C_a = C_ox
	C_ox + C_W

In acuumulation there is no depletion layer and in this case, the total capacitance reduces to C_ox. Once a depletion zone is formed, the capacitance depends on the frequency. For low frequencies, the generation-recombination current causes a short circuit of the depletion capacitance and the capacitance reduces to C_ox. See Fig. 7 on p. 371 of Sze

or Fig. 4-3-5a on p. 348 of Shur

. For high frequencies, the depletion zone is not short circuited and the measured capacitance is a series capacitance of the oxide and the depletion width. The depletion width is constant once it is fully formed (see images above) and we will measure a constant capacitance.

Field Effect Transistor (FET)

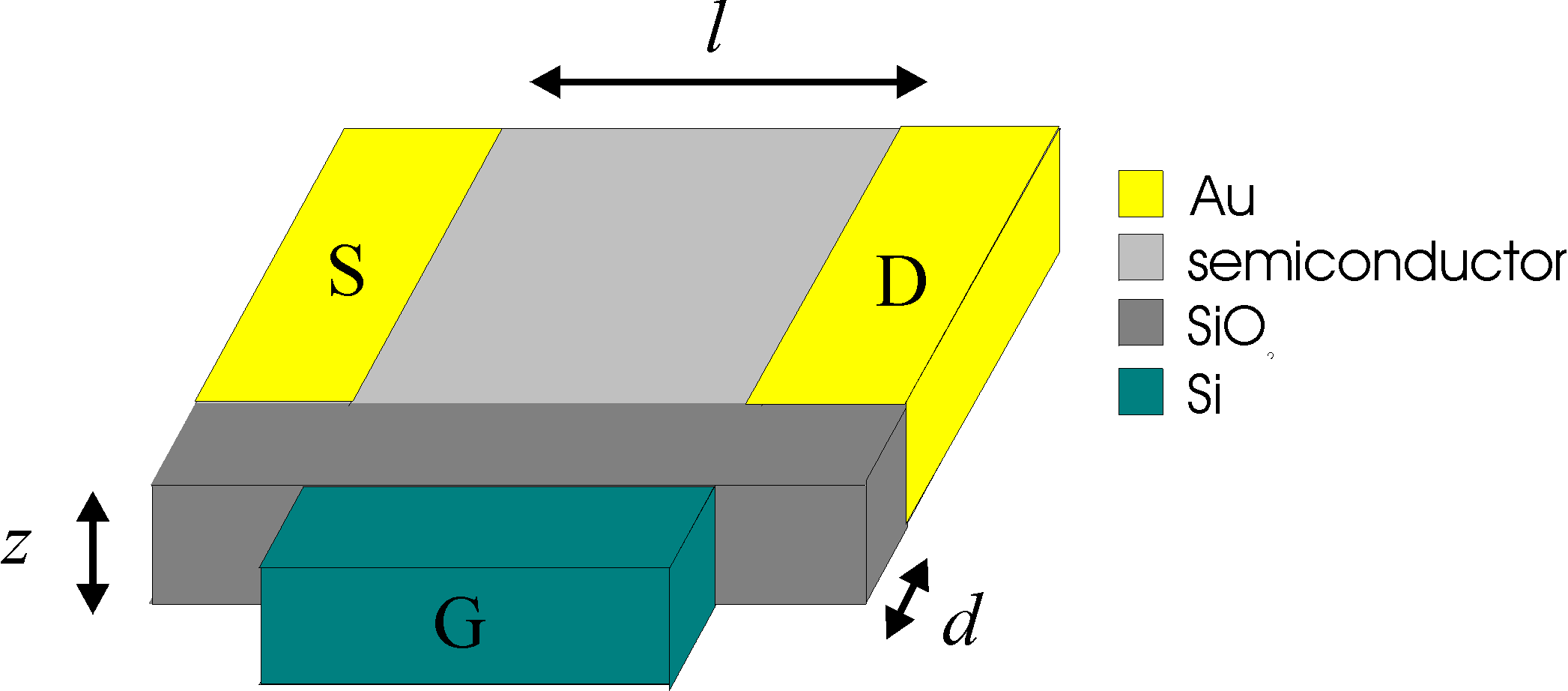Directions:
x: from oxide to surface of film
y: from source to drain
z: along an electrode

Z: electrode width
L: electrode distance
d: oxide thickness

An FET is nothing more than an MIS device with electrodes connected on two lateral sides of the semiconductor. Imagine connecting an electrode above and one below the images above. The first one we will call the source, the latter the drain.
The total current through this device is then linearly proportional to the number of free carriers in the semiconductor. The other parameters are the mobility m, the external electrical field E_x: and the device dimensions Z and L: I_DS = Z|Q|mE_x= Z|Q| mV_y/L ( I ) with I_DS the total current, m the mobility of the carriers, V_y the external voltage (is equal to V_DS), Z the width of an electrode, L the distance from source to drain, and |Q| the amount of free charge in a line perpendicular to the oxide surface (along x) in C/m². This is equal to integrating the electron and hole density (ignoring the sign) from the edge of the oxide to infinity (or to the limits of the semiconductor film), see the figure with free carriers above.
In case we have substantial contributions from both electrons and holes, and they have different mobilities, we have to replace the part |Q|m with (|Q_p|m_p + |Q_n|m_n).
We will see that this can explain the linear region of an FET. To calculate the IV curves in the linear region, we only have to calculate the number of free carriers. For the saturation region the equations are a little different, as will be shown later.

Linear region

As a first order we can say that we only have free carriers when we are in strong inversion or strong accumulation. As can be seen from the strip of figures above, we need to supply a certain voltage to the gate to induce either strong inversion or strong accumulation.This is the so-called threshold voltage V_T. This doesn't mean that we don't have free carriers and conduction below this threshold voltage, but that the conduction beyond this voltage is much larger.

Under the assumption that all the free carriers come from charges in the strong accumulation or depletion zone, it is very easy to calculate the amount of charge on the semiconductor side and hence the current. In the section above we have seen that the capacitance of an MIS junction under these conditions is equal to the oxide capcitance, C_ox. Assuming no other capacitances, all the charges go to the interface and therefore, since C = Q/V we find Q = C_ox V_G. As written above, we need V_T to bring it into strong accumulation or depletion, therefore Q = C_ox (V_G-V_T). With this in mind, and with the idea that the conduction is proportional to the charge as seen in equation I the current in the linear region becomes

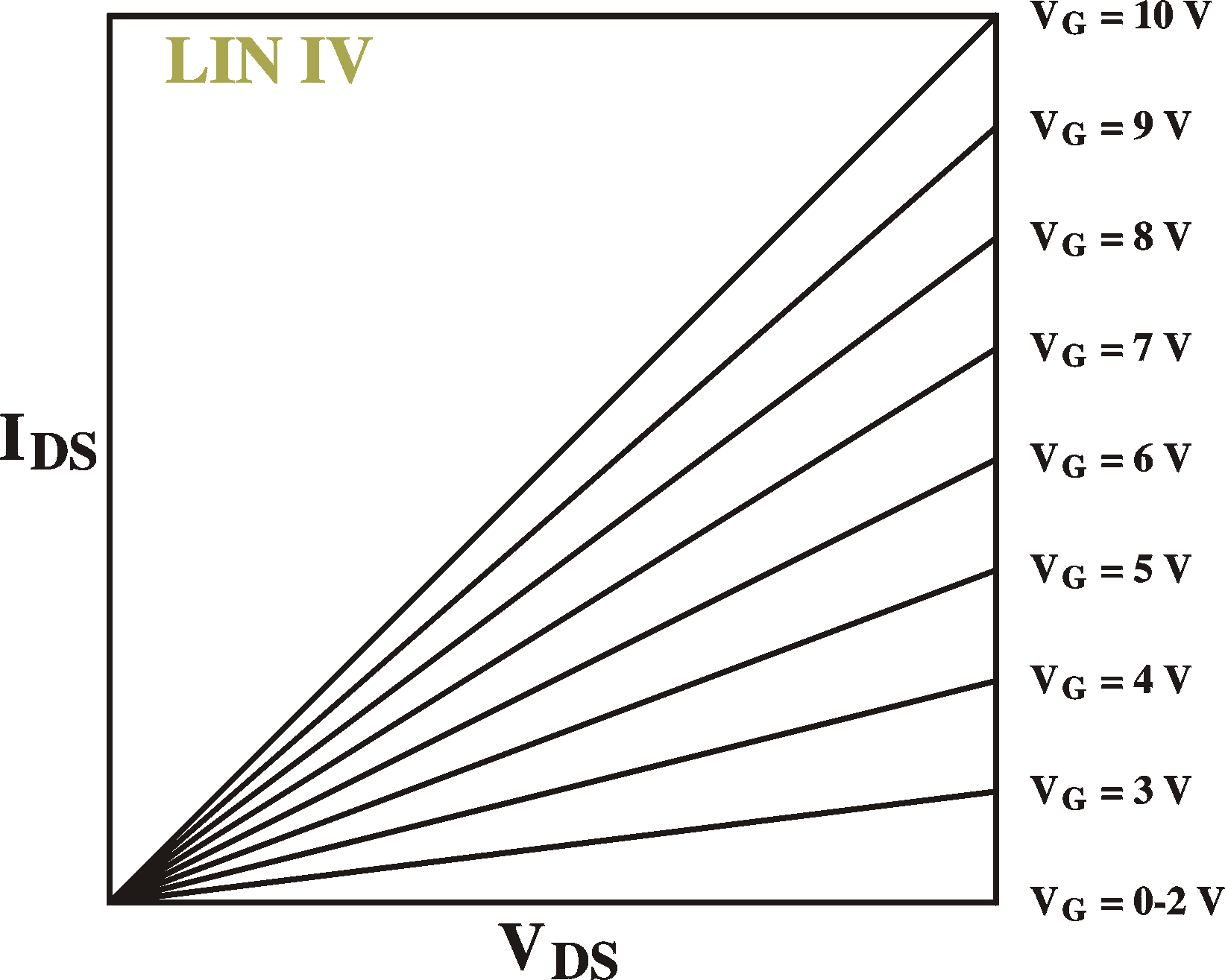
I_DS = C_ox (V_G-V_T) mV_DSZ/L

Examples of IV curves (I_DS vs. V_DS; left) for different gate voltages and transfer curves (I_DS vs. V_G; right) for different drain-source voltages. V_T = 2 V.

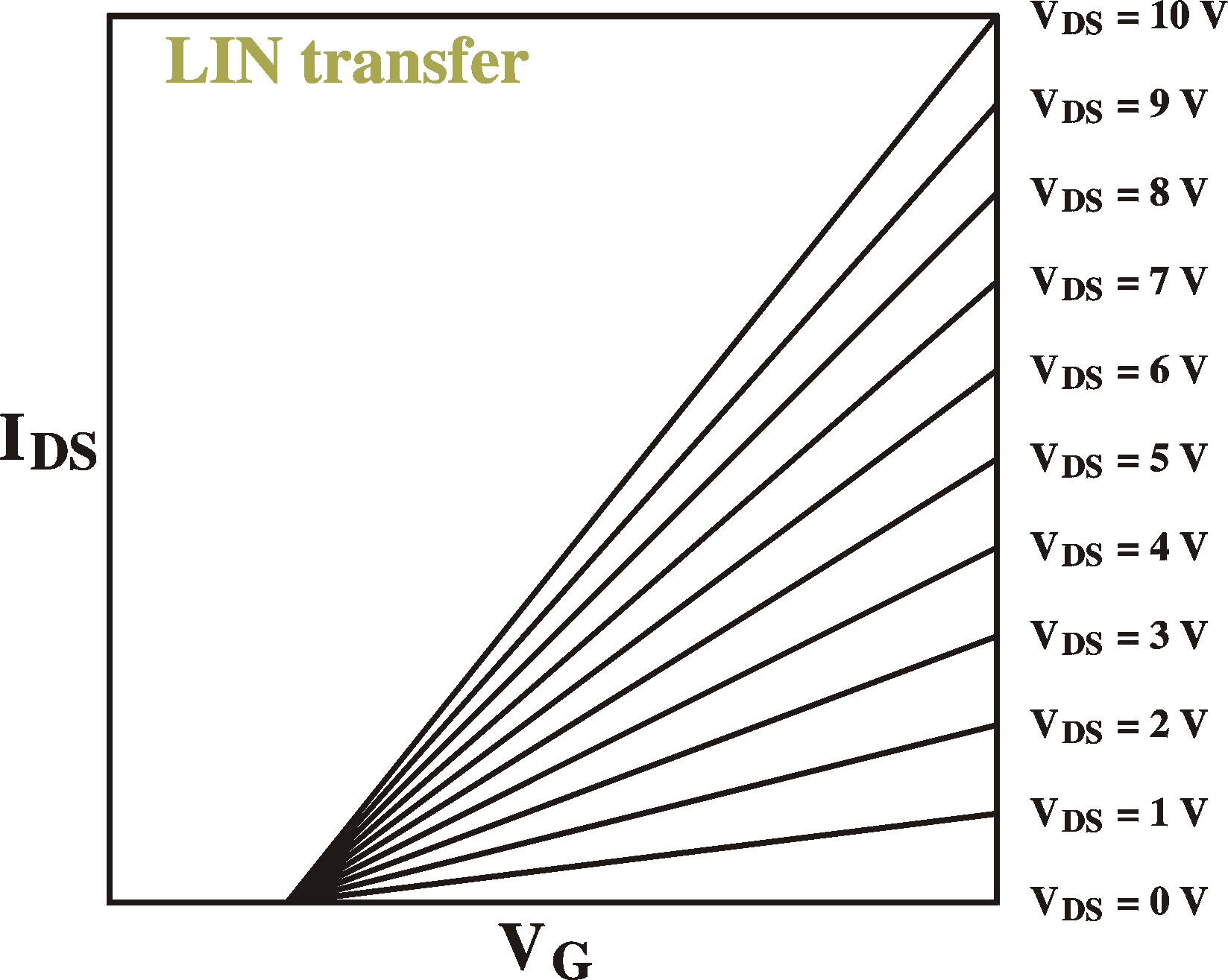Remember that we arrived at this by the assumption that all the free carriers are located in the strong inversion or accumulation zone close to the interface and that the rest of the device is not conducting. Especially in materials with bulk Fermi levels close to the band edges, the background conductivity (the "off current") can be very large. In principle, the purer the material, the closer the Fermi level will be to mid gap and the less off-current we will have. Making the films thinner also helps.
Moreover, not all the charge induced by the gate is free charge. The above model is also known as the Charge Control Model. If we do include the background conduction in the bulk and the depletion and inversion zones, we have to add a term to the above equation, to arrive at the Schottky model, see Sze and Shur .

Threshold voltage of an inversion-channel FET

Following the above discussion and the MIS strip of figures, it is clear that the band bending cannot be larger than the bandgap before either strong accumulation or strong inversion occurs. In other words, at the onset of strong inversion, the band bending V_bb is exactly equal to the difference between the conduction band and the Fermi level, (E_C-E_F)/q in the bulk.The depletion width is then (see section on Schottky barrier) W = (2e_sV_bb/ qN_A)^1/2. The electrical field at the interface is the integral of the space charge inside this depletion region: E_max = (qN_A/e_s)W = (qN_A2V_bb / e_s)^1/2.
Maxwell's equations tells us that, in the absence of any charge, the displacement D (=eE) is continous accross the interface. On the semiconductor side of the junction we have D_s = e_s(qN_A2V_bb/ e_s)^1/2. In the oxide we therefore have an electrical field of E_ox = (1/e_ox)(qe_sN_A2V_bb)^1/2. This field is constant inside the oxide because there are no net charges there. We therefore have an extra voltage drop of DV = d_oxE_ox = (d_ox/e_ox)(qe_sN_A2V_bb)^1/2 accross the oxide. The total external voltage then becomes (d_ox/e_ox)(qe_sN_A2V_bb)^1/2 + V_bb = V_T.. With V_bb equal to (E_C -E_F)/q this becomes V_T = (d_ox/e_ox)[2qe_sN_A(E_C-E_F)/q]^1/2 + (E_C-E_F)/q Remember that C_ox = e_ox/d_ox, and, in normal cases, the Fermi level is very close to the valence band, so that (E_C-E_F)/q = E_G/q which we can call 2y_B. With this in mind, the above equation becomes the following text book equation for an n-type inversion channel:

V_T = (4qe_sy_BN_A)^1/2 / C_ox+ 2y_B

As an example: for N_A = 1x10¹⁶ cm^-3, C_ox = 50 mF/m², E_G = 2.5 eV (y_B = 1.25 V), e_s = 5.0e₀ we get V_T = 11.9 V + 2.5 V = 14.4 V; since the first term in the equation comes from the oxide and the second term comes from the semiconductor we can see that most of the external voltage (83%) is absorbed by the oxide (remarkably).
The Fermi level, of course, also depends on the acceptor concentration, so in total we get a complex dependence on N_A. In textbooks, it is assumed that all acceptors are ionized. In fact, for organic materials, where the acceptor level can be very deep (but abundant) this is not necessarily the case. In fact, we should read N_A as "ionized levels" and this can be a fraction of the real number of acceptors, unlike in classical materials such as Si and GaAs. Moreover, the fraction of levels ionized can be changed by changing the band bending (by applying a gate voltage) and thus, the threshold voltage can change when putting the device in operation. Depending on the depth of the levels, these changes can be in the order of seconds, to minutes and hours and even days.
Note that high levels of current have no effect on this trapping of charges, since they do not attribute to a different band bending or extra charges in the interface.
Note that for an accumulation type FET this calculation does not work because we do not have a space-charge region caused by ionized acceptor levels; V_T does then not depend on N_A., but only on the Fermi level and the number of valence band states.

Remark: We have considered here an FET without a wire connected to the bulk of the device. If we do so, the threshold voltage reduces to V_T = (2qe_s(y_B-V_sub)N_A)^1/2 / C_ox+ 2y_B, with V_sub the voltage of the substrate.

Subthreshold region of an inversion-channel FET

The subtreshold region is the region of gate voltages before the channel is opened. The desnity of free carriers at the interface is exponentially depending on the distance between the conduction band and the Fermi level. When the channel is formed, the Fermi level remains fixed (resonant) at the edge of the conduction band. Further increases in voltage result only in a tiny shift of E_F; only minute changes in E_F are needed to create free charges C_ox(V_G-V_T). In the subthreshold region the distance E_F-E_V is determined by the gate voltage and the acceptor concentration in the bulk in the following way (very similar to the calculation of the threshold voltage above):
1) Poisson's equation tells us that the band bending in the semiconductor is equal to double-integral of the density of ionized acceptors: V_bb = double-integral N_A
2) This will tell us the field at the interface and hence
3) The field and voltage drop in the oxide and hence the
4) Total voltage drop in the device.
5) Reversing these calculations, if we know the total voltage accross the device, we will also know the band bending in the semiconductor.
6) If we know the band bending in the semiconductor and we know the initial distance between Fermi level and conduction band, we will know the position of the Fermi level at the interface.
7) If we know the position of the Fermi level at the interface, we know the density of free carriers at the interface (Fermi-Dirac distribution, which is more or less exponential)

If you do the calculation correct, you will see that the distance of the Fermi level depends linearly on the gate voltage and with a square-root on the acceptor density N_A. Hence the current follows something like (Sze , Szur )

I_ds = I₀ exp[V_G/ square root

N_A]

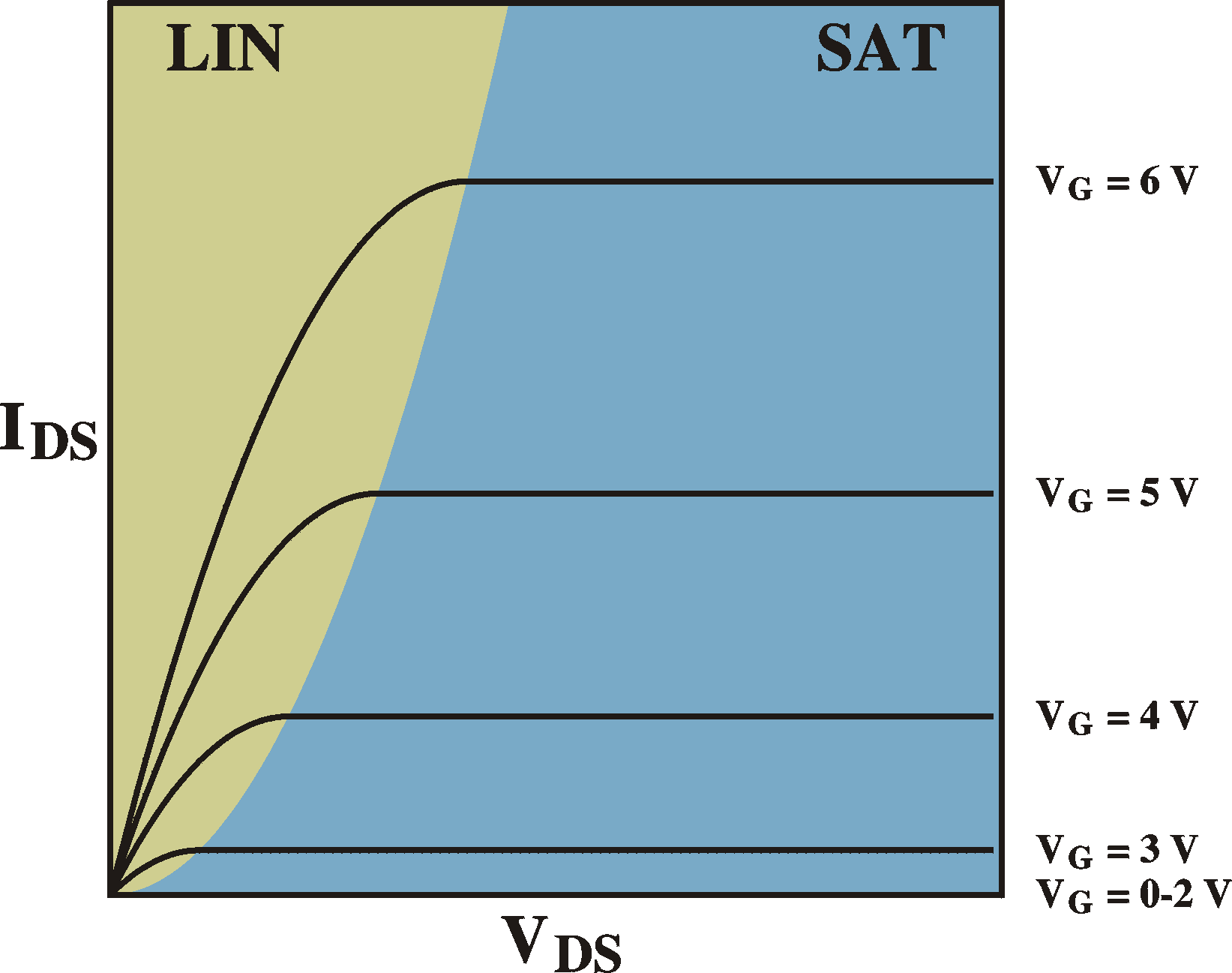
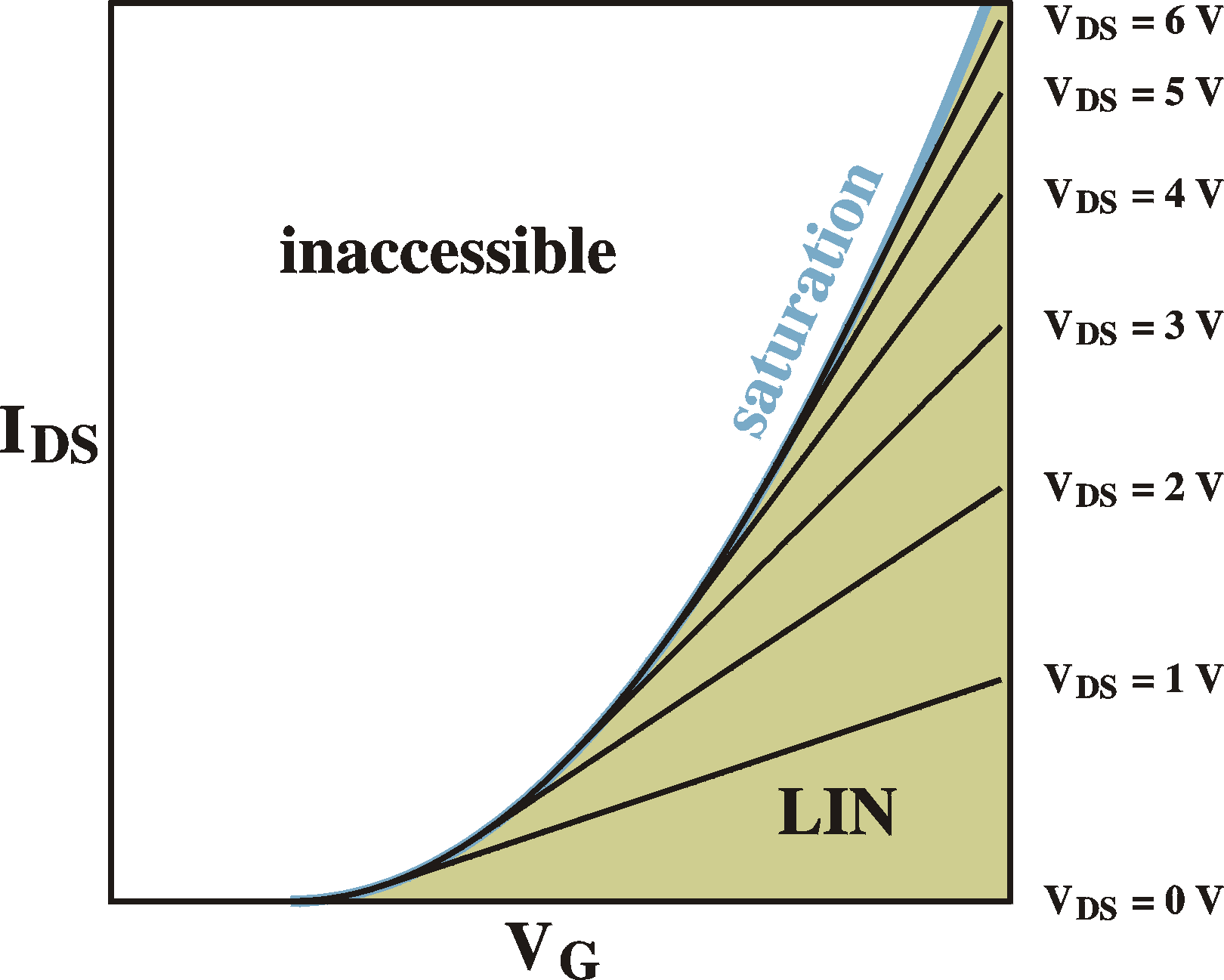
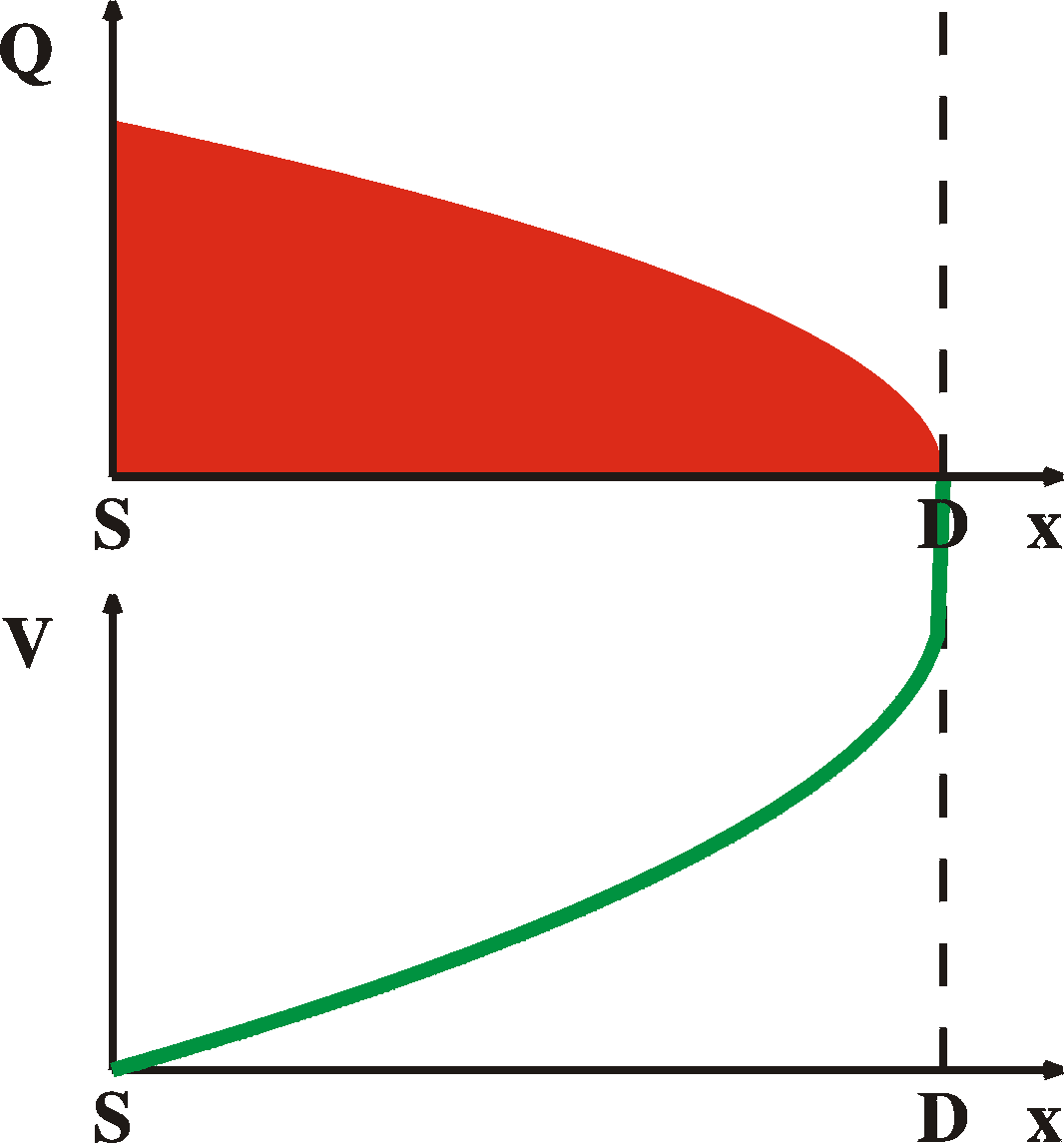
Saturation

If we increase the drain-source voltage eventually we will go into saturation where the current becomes independent of the drain-source voltage It is very easy to understand why this should happen. Imagine an FET with a threshold voltage of V_T = 1 V. We will apply a gate voltage well beyond this value, let's say 10 V. The channel is therefore open. For low drain-source voltages, both the drain and the source and hence the entire bulk region of the device is at 0 V, or close to 0 V at all places. At the drain, the gate-drain voltage is 10 V and this is well beyond the threshold voltage. Here we have a conducting channel. At the source (which is always at 0 V), the gate-source voltage is also 10 V and here the channel is also open. Actually, at all places do we have a conductive channel.
Let us now set the drain voltage to 10 V. At the source we still have a gate-source voltage of 10 V and the band bending here will still induce a channel. However, at the drain, the gate and the drain are at the same voltage; the gate-drain voltage is 0 V and this is below the threshold voltage for creating a conductive channel. The channel is closed here. This we call pinch-off.

If we assume a linear voltage drop from source to drain from 0 to 10 V, we can exactly calculate where the channel closes, namely at 10% distance from the drain. We have to bear in mind, though, that a closed channel has less free carriers and thus has higher resistivity. The law of continuity tells us that the current at every place of the device must be equal. Therefore, since voltage drop is current times resistivity, the voltage drops much faster in a closed-channel region than in a open-channel region. Moreover, if we assume that the free-carrier density in the closed-channel region is much smaller than the open-channel region, the pinch-off region is very small.

The voltage of start of saturation is easy to calculate. At this voltage the gate-drain voltage is exactly equal to the threshold voltage. V_G-V_D = V_T. Thus (V_S = 0, V_D = V_DS)

onset of saturation: V_DS = V_G-V_T

Beyond this voltage, the current is constant. We will have a region from the source to near the drain with a voltage drop of V_G-V_Tand a very thin region close to the drain with the rest of the voltage drop of VDS. The length of the first region is nearly independent of the total external voltage. It therefore has a contant length and voltage drop, and the current through it is therefore independent of V_DS. Again, continuity tells us that the current at every point is equal, therefore, the saturation current is independnet of V_DS.

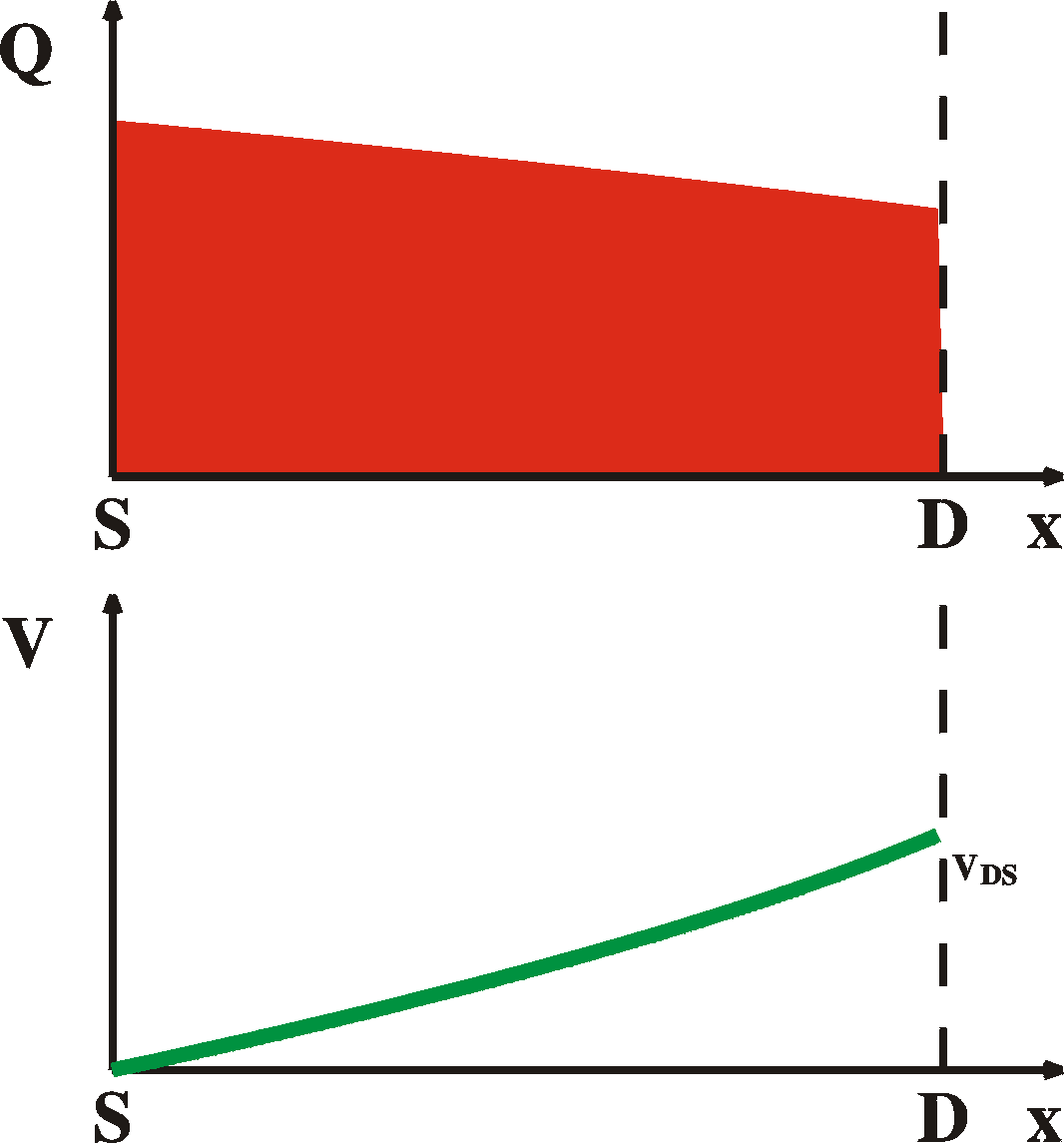
With this we can calculate the free carrier density Q(x) and the voltage V(x) of every point in the channel at the onset of saturation. Along the way we will also calculate the current which is the current in saturation.
Imagine putting up a screen at a distance x from the source, peprpendicular to the source-drain direction, stretching as long as the electrode lengths (Z) and as high as the film thickness. We can calculate the current I through such a screen.
The current I at a crossection at a certain point x is equal to the free-charge density at that point Q(x), the carrier mobility m and the local field E(x) = dV(x)/dx:
    I(x) = ZmQ(x) dV(x)/dx
Because of continuity, this current has to be constant along x and equal to the drain-source current I_DS. The above equation then reduces to
    dV(x) / dx = I_DS/ZmQ(x)         (eq.I)
The free-carrier density is a function of the local field V_G-V(x), as seen before:
    Q(x) = C_ox[V_G-V(x)-V_T]       (eq.II)
The solution to this system of diferential equations is easy (take the derivative of the second equation and put this in the first), to which we add the following boundary condition:
    1a: the charge at the drain is zero: Q(L) = 0.
    1b: The voltage at the drain is just enough to close the channel: V(L) = V_G-V_T.

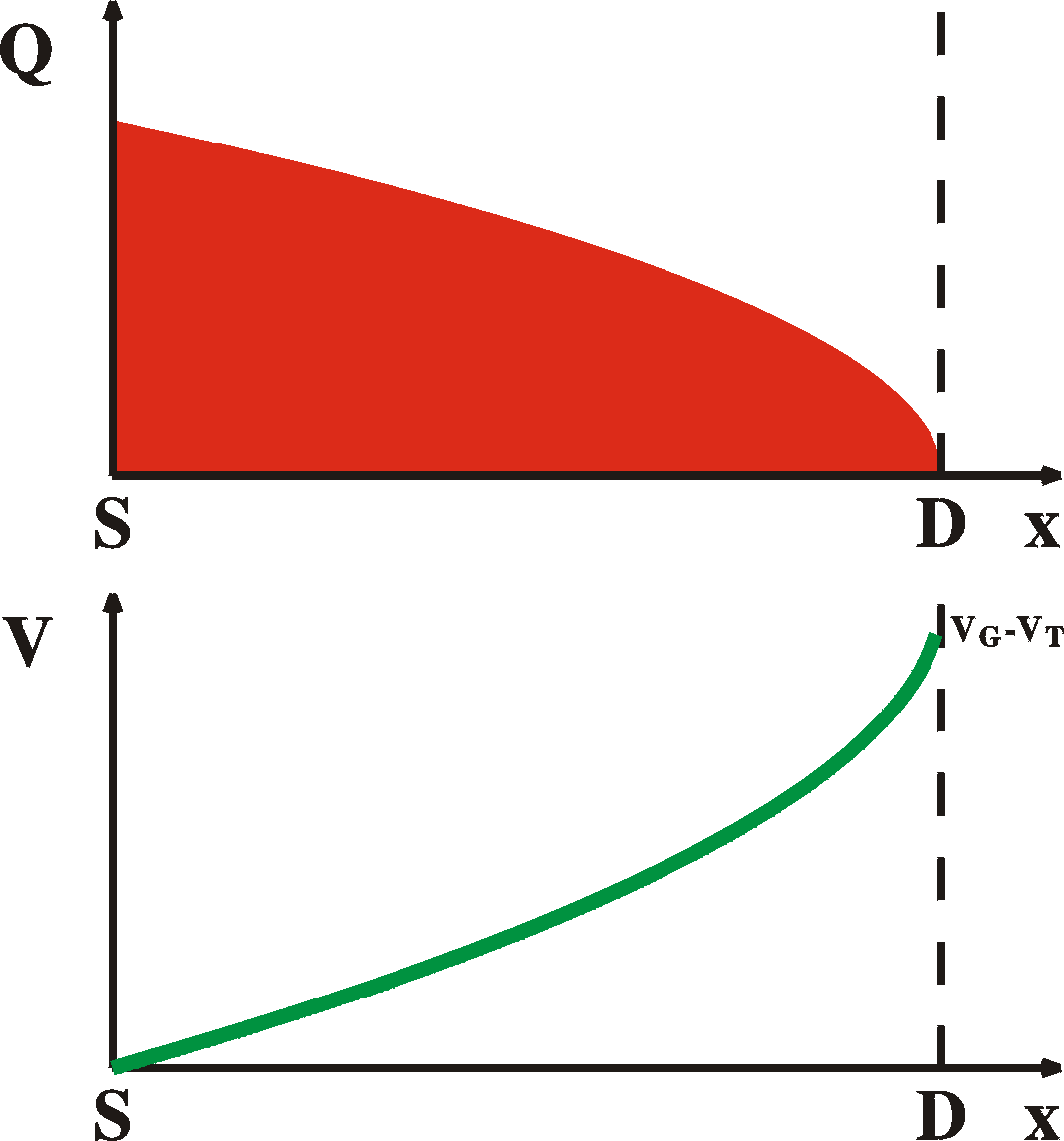Sta Vnq The soulution is then
    Q(x) = [(2C_oxI_DS/Zm)(L-x)]^1/2
    V(x) = (V_G-V_T) - [(2I_DS/mZC_ox)(L-x)]^1/2
Using the next boundary condition
   2a: The voltage at the source is 0: V(0) = 0
   2b: The charge at the source is Q(0) = C_ox (V_G-V_T)
we can calculate the current

I_DS = (1/2)m(Z/L) C_ox (V_G-V_T)²

which is the current at the onset of saturation and, since, as we have shown before, the current beyond this point is independent of V_DS, this is the current in saturation (as long as V_G < V_DS + V_T).
The total amount of charge stored in the device in saturation can be found by integrating the equation for the charge distribution above and multiplying by the device width Z:
at saturation, V_DS = V_G-V_T: Q = (2/3) Z (V_G-V_T) C_ox
in the same way:
at V_DS = 0 V : Q = Z (V_G-V_T) C_ox
Note: when we increase the bias, charge is coming out of the device. We have to be careful in our IV measurements that we do not measure the current of these charges going into and coning out of the device. See the section on displacement current.

We can also use the same method to calculate the current before saturation. Going back to the general solution of the system of differential equations:
    V(x) = (V_G-V_T) - [(2I_DS/mZC_ox)(x₀-x)]^1/2
As boundary conditions we now take:
    1: The voltage at the source is 0; the charge is C_ox (V_G-V_T)
    2: The voltage at the drain is V(L) = V_DS
The result is

I_DS = m(Z/L) C_ox [(V_G-V_T)V_DS- (1/2)V_DS²]

which is equal to what we found for the linear region, except for the term V_DS² which becomes important only when we approach saturation. When we susbtitute V_DS << V_G-V_T we get the equation for the linear region. When we substitute the saturation condition V_DS = V_G-V_T we reproduce exactly the equation for saturation currents.

Examples of IV curves (I_DS vs. V_DS; left) for different gate voltages and transfer curves (I_DS vs. V_G; right) for different drain-source voltages. V_T = 2 V.

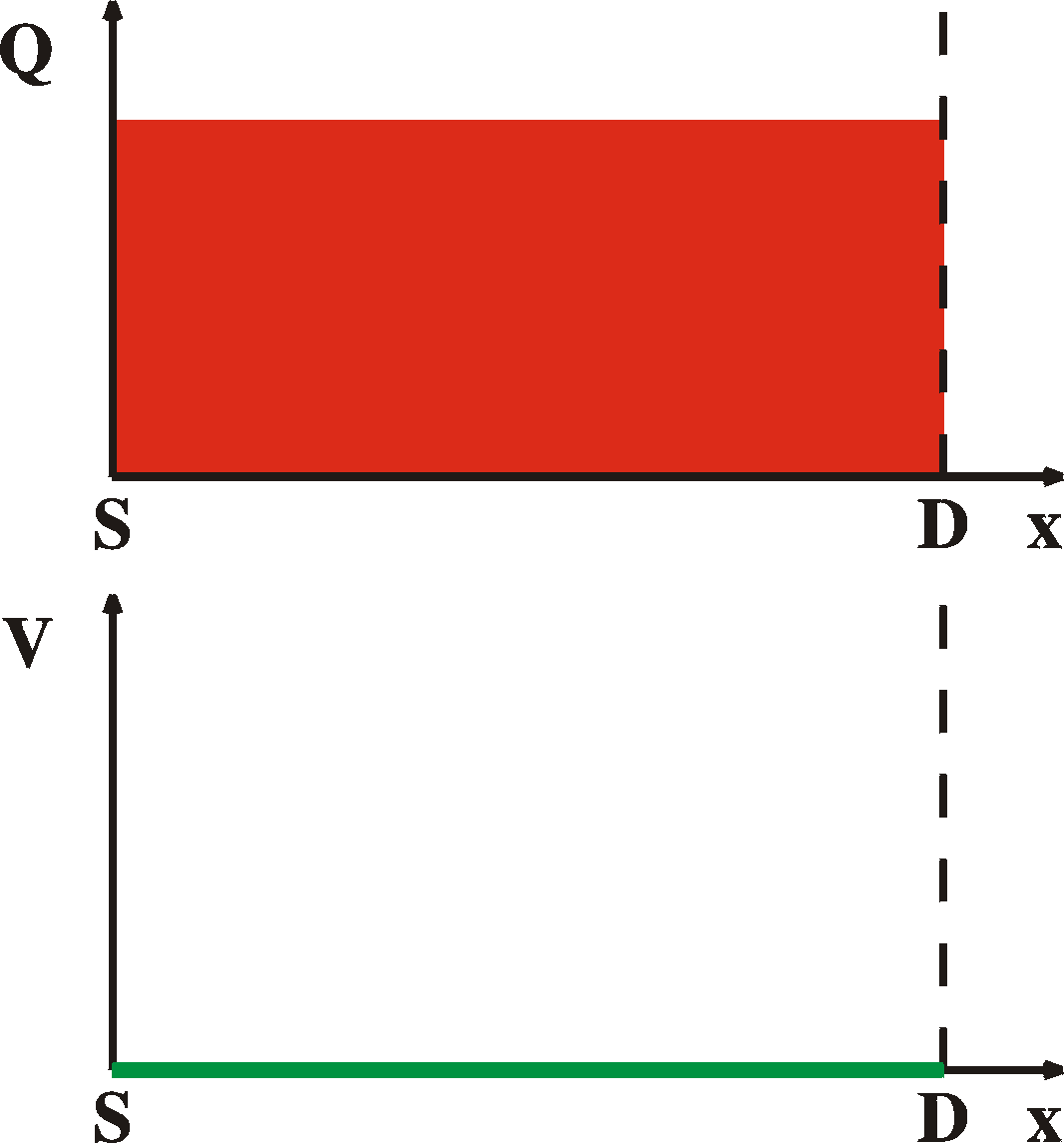
For completeness sake and for later reference, here are the charge distributions and voltage curves for the different regimes, ranging from 1) equilibrium, 2) linear regime, 3) onset of saturation, 4) in saturation.

No bias Onset saturation

V_DS = 0 V V_DS < V_G-V_T
LIN V_DS = V_G-V_T
onset of SAT V_DS > V_G-V_T
SAT

Short-channel effects

For short channels we can expect the following:
Non saturating saturation currents. We assumed that the voltage drop along the channel is comprised of two parts, a gradual drop V_G-V_T independent of V_DS over nearly the entire channel and the last part [V_DS-(V_G-V_T)] completely absorbed by an infinitesimal small region. When the channel becomes shorter, the last part takes relatively more space and we cannot assume anymore that the voltage drop V_G-V_T occurs over a constant amount of space independent of V_DS. In fact, this region becomes ever smaller and the field will proportionally increase, together with the currents. In other words, the current is, in saturation no longer independent of V_DS. See Fig. 41 on p.478 of Sze.
We can easiliy explain this. At the source and the drain we have a depletion region (a zone without free holes in an n-p-n inversion channel FET). This zone will absorb the entire voltage drop V_DS-(V_G-V_T). Normally these zones are thin compared to the bulk. It is easy to calculate the width of these depletion zones (see the section on Schottky barriers):
y_s = [2e_s/qN_A (V_bi-y_s)]^1/2
y_d = [2e_s/qN_A (V_bi-y_s+V_D)]^1/2
for the depletion width at the source and drain respectively. Note that they also depend on the gate; once the channel has formed, the depletion width at the source disappears, but we still keep a depletion width at the drain which will absorp the excess V_DS. Note that this "barrier" at the drain doesn't hinder the current, because it is in the forward direction for "minority carriers" (electrons for npn device).
When this depletion width becomes comparable to the channel length we can expect short-channel effects. This also depends on the acceptor concentration.
Non-zero subthreshold currents. Before threshold, we have pn-junctions on either side of the semiconductor. The depletion width W of these follows the standard calculations. When the channel length is decreased, these depletion regions can start overlapping. This will cause that the currents increase. This is easy to see why. When a carrier is injected by diffucsion over the first barrier, into the "channel", it immediately starts feeling the fields of the second barrier on the other side and is pulled away to that electrode; it has a significant chance of making it to the other side. In fact, the diffusion (space-charge limited current) will dominate and the currents will be of the form J = V_DS².
Threshold voltage shift.
Because trapping of charges takes places, the current continuously drops. To compensate for this, a larger voltage has to be applied at the gate to keep the same amount of mobile charges in the channel.

References

Scientific American, July 1995.
Physics of semiconductor devices, S.M. Sze, 2nd edition, John Wiley & sons, 1981, ISBN 0-471-05661-8
Physics of semiconductor devices, M. Shur, Prentice Hall, 1990, ISBN 0136664962
The Electrical Characterization of Semiconductors : Majority Carriers and Electron States (Techniques of Physics, Vol 14) by P. Blood, J.W. Orton, ASIN: 0125286279
Advances in Sythetic Metals, Twenty years of Progress in Science and Technology. ed. P. Bernier, S. Lefrant and G. Bidan, Elsevier (1999).
Fabrication and characterization of electronic devices based on poly(3-methylthiophene), H.L. Gomes, PhD thesis, University of Wales at Bangor, 1993.
Electronic levels in MEH-PPV, ICEL-2 Conference, Sheffield. P. Stallinga, H.L. Gomes, H. Rost, A.B. Holmes, M.G. Harrison, and R.H. Friend. Accepted for publication in Synthetic Metals.
Deep-level transient spectroscopy: A new method to characterize traps in semiconductors, D.V. Lang, J. Appl. Phys. 45, 3023 (1974).
Charge carrier transport in poly(p-phenylenevinylene) light-emitting device, S. Forero, P.H. Nguyen, W. Bruetting, M. Schwoerer, Phys. Chem. Chem. Phys. 1, 1769 (1999).
S. Karg, J. Steiger, and H. von Seggern, ICEL-2, proceedings, accepted for publication in Synthetic Metals (1999), and references therein.
Microelectronic Circuits, A.S. Sedra, K.C. Smith, 4th edition, Oxford University Press, New York (1998).
Electronic Devices and Circuits, T.F. Bogart Jr., 4th edition, Prentice Hall, Upper Saddle River (1997).
Interface state mapping in terrylene, P. Stallinga, H.L. Gomes, M. Murgia, K. Müllen, Organic Electronics 3, 43 (2002).
Electrical Characterization of FETs of sexithiophene, P. Stallinga, H.L. Gomes, F. Biscarini, M. Murgia, J.Appl.Phys. (2004).
Gate voltage dependent mobility of oligothiophene field-effect transistors, G. Horowitz, R. Hajlaoui, D. Fichou, A. El Kassmi, J. Appl. Phys. 85, 3202 (1999).
Theory of the field-effect mobility in amorphous organic transistors, M.C.J.M. Vissenberg, M. Matters, Phys. Rev. B 57, 12964 (1998).
Organic field-effect transistors, G. Horowitz, Adv. Mater. 10, 365 (1998).
Electrical properties of single crystals of rigid rodlike conjugated molecules, J.H. Schön, Ch. Kloc, R.A. Laudise, and B. Batlogg, Phys. Rev. B 58, 12952 (1998).
Bias-induced threshold voltages shifts in thin-film organic transistors, H.L. Gomes, P. Stallinga, F. Dinelli, M. Murgia, F. Biscarini, D.M. de Leeuw, T. Muck, J. Geurts, L.W. Molenkamp, V. Wagner, Appl. Phys. Lett. 84, (2004).
For the physical constants I relied on the very useful CERN pages

http://pdg.lbl.gov/2000/contents_sports.html

et al.

In the text the following variables and constants were used:

variables
variable	description	unit
A	area of the interface	m²
b	temperature scanning speed	K/s
C	capacitance	F
C₀	background capacitance or DC capacitance	F
DC	capacitance-transient amplitude	F
c_p	hole capture rate	1/s
e	electrical permittivity	F/m
e_p	hole emission rate	1/s
E	electric field	V/m
E_pa, E_A, E_A1, E_A2, E_b	activation energies	J
E_F	Fermi level	J
E_VB, E_CB	valence-band level and conduction-band level	J
f_m	(metal) work function	J
G	conductance (1/R)	1/W
I	current	A
J, J₀	current density	A/m²
N_T, N_A, N_D	impurity densities	1/m³
Q	total space charge	C
R, R_b, R_d	resistance	W
r	charge density	C/m³
S	DLTS signal	F

variables
variable	description	unit
T	temperature	K
t, t₁, t₂	time	s
t, t₀	life time or decay time	s
V_bi	built-in voltage	V
V_bb	total band bending	V
V, V_E, V_F	applied external voltage	V
V_n	Fermi level depth in semiconductor relative to conduction band	V
W	depletion width	m
w, w₀	radial frequency	rad/s
x	space coordinate	m
c	electronaffinity	V

constants
constant	description	value	unit
e₀	permittivity of vacuum	8.854187817 ....10^-12	F/m
h	Planck constant	6.6260755(40) 10^-34	Js
k	Boltzmann constant	1.380658(12) 10^-23	J/K
q	elementary charge	1.60217733(49) 10^-19	C

Note: the units presented here are according to S.I.
In reality often different units are encountered. For
instance, energies are nearly always given in eV
(1.6 10^-19 J) , depletion widths in nm or Å
and impurity levels in cm^-3

page written and maintained by Peter Stallinga

Source written in HTML with NetScape 4.76. Pictures made with PjotrSoft (my software name), output in PostScript format. Converted with Corel Draw, GhostView, LViewPro and GIMP (Linux) into GIFs.
In no way were any electrons harmed in the process!
Copyright © 1999-2007, Universidade do Algarve

a) Depletion	When a small (positive) voltage is connected to the metal (gate), free holes are pushed out of the interface region and a band bending results on the other side of the insulator. This is the same effect as seen in a Schottky barrier. Free carriers (holes) flow out of the interface region and a depletion zone is formed. The uncompensated (negatively) ionized acceptors cause an electric field and - via Poisson's equation - a parabolic bending of the bands. Note that there is also a voltage drop in the oxide. In the oxide no charges can reside and hence the field is constant and the voltage drop is linear in space. The total voltage drop in the oxide plus the band bending is equal to the external voltage.
b) Inversion	When the voltage is further increased, at the interface an inversion region is created. The semiconductor becomes here n-type, albeit not very conductive, yet.
c) Strong Inversion	For very strong bias, the Fermi level crosses the conduction band close to the interface. This is strong inversion. Free electrons are in a so-called "channel" next to the oxide. This channel is therefore highly conductive. The ample availability of states in the conduction band means that further increases in the gate voltage will not extend this strong inversion region into space, but rather will increase the density of electrons in the channels. The channel is always infinitesimally thin.The huge amounts of free carriers can easily cause a large voltage drop (band bending) and only a thin layer is needed to "absorb" the external voltage. Note that the depletion width (the white zone) and the inversion width (light blue zone) are constant once the channel is formed.
d) Accumulation	Going in the other direction, a negative voltage at the gate metal will attract some free holes to the interface. In this accumulation region, an increased number of free holes is created, although it is not yet dramatic; the interface is still high-ohmic.
e) Strong accumulation	For stronger negative voltages at the gate the Fermi level is forced below the valence band at the interface. A channel with high density free holes is created. This is called strong accummulation. Again, as for the strong inversion case, further increasing the voltage will result in an increase of the density of the free holes rather than an increase of the channel in space. In the picture the width of the channel is exaggerated. In reality it is only a monolayer thick.


V_DS = 0 V	V_DS < V_G-V_T LIN	V_DS = V_G-V_T onset of SAT	V_DS > V_G-V_T SAT