
No, we do not have
a political agenda. We are a non-profit science
organization!
This research gets funding from nobody!
|
Feedback
A simple model of
greenhouse effect can predict a temperature sensitivity
of 0.1-0.4 degrees for doubling of CO2 in the
atmosphere. This falls far below the predictions of
IPCC. How can that be? What is the trick? |
|
First of all, let's explain feedback theory. Imagine
you have a system where the output signal y (for instance
temperature) is determined by the input signal x (for instance CO2
concentration) and that there is a gain (or sensitivity) A between the two:
Now we add feedback, stating that part of the output signal y is added to the input with a factor β
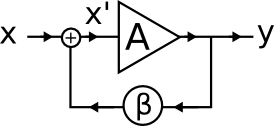
The overall gain of this
system is then
You can see that the output y can be arbitrarily large for a careful selection of parameters A and β. Now you understand how the IPCC can simulate any temperature variation based on any CO2 variation with a careful choosing of only two parameters, namely A and β. It is as simple as that. They can even, should the need arise, predict 100-degrees temperature rises.
If in 1998 it is very warm, these parameters are adjusted to retroactively predict the temperature. Then, in their reasoning, the temperature of 1998 is seen as proof of the correctness of the parameters and any predicted subsequent rise on basis of these parameters seen as unavoidable.
That while their entire idea of feedback does not make sense. Why? Read further
The above is an example of positive feedback (if β>0) and will typically result in a runaway system. Every cycle through the loop (which can take some time in real life) will increase the overall amplitude of the output y. Imagine I look at my bank account and add every day the amount that is already there (Aβ=1). I start with 1 euro. Next day I will add 1 and have 2 euros. Then 4, then 8 ... etc. This is a runaway system. Adding every day twice the amount of money already there is equally a runaway system (1, 3, 9, 27, ... ).
It is only stable if Aβ<1. In which case the system is stable, and the amplitude y can only be large for values close to 1. The IPCC talks about "the system is unstable and we are reaching a critical point of no return", showing that indeed this is their way of analyzing the climate system; their parameters are indeed close to 1 (stable, but large amplitude) or even beyond 1 (runaway). The sheer probability of Aβ being close to 1 is astronomically small, never mind that that can make them simulate a tiny fragment of the climate history. Moreover, we would have observed quite different climate phenomena in the past.
For negative feedback, however, Aβ<0, the system is stable. Any deviation from a stable situation would have 'forces' bringing the system back to the stable situation. And this must be the case. All the time the climate system is brought off-balance by: seasonal (summer and winter) fluctuations, daily (day and night) fluctuations, random (weather) fluctuations, incidental (volcanic) events. The climate always recovers.
It is impossible to have large positive feedback (Aβ>1). It is highly unlikely to have positive feedback at all (Aβ>0). It is very likely there is negative feedback (Aβ<0).
This means that the resulting amplitude, y = A/(1-Aβ) x, is smaller than what can be expected without feedback, because A/(1-Aβ) < A. We can thus expect a climate sensitivity of CO2 smaller than 0.1 degrees for doubling CO2 in the atmosphere. The exact value can be a point of discussion.
For more information, contact me at The University of The Algarve,
y = A x
Now we add feedback, stating that part of the output signal y is added to the input with a factor β
y = A x'
x' = x
+ β y

y = A/(1-Aβ) x
You can see that the output y can be arbitrarily large for a careful selection of parameters A and β. Now you understand how the IPCC can simulate any temperature variation based on any CO2 variation with a careful choosing of only two parameters, namely A and β. It is as simple as that. They can even, should the need arise, predict 100-degrees temperature rises.
If in 1998 it is very warm, these parameters are adjusted to retroactively predict the temperature. Then, in their reasoning, the temperature of 1998 is seen as proof of the correctness of the parameters and any predicted subsequent rise on basis of these parameters seen as unavoidable.
That while their entire idea of feedback does not make sense. Why? Read further
Positive feedback vs. negative feedback
The above is an example of positive feedback (if β>0) and will typically result in a runaway system. Every cycle through the loop (which can take some time in real life) will increase the overall amplitude of the output y. Imagine I look at my bank account and add every day the amount that is already there (Aβ=1). I start with 1 euro. Next day I will add 1 and have 2 euros. Then 4, then 8 ... etc. This is a runaway system. Adding every day twice the amount of money already there is equally a runaway system (1, 3, 9, 27, ... ).
It is only stable if Aβ<1. In which case the system is stable, and the amplitude y can only be large for values close to 1. The IPCC talks about "the system is unstable and we are reaching a critical point of no return", showing that indeed this is their way of analyzing the climate system; their parameters are indeed close to 1 (stable, but large amplitude) or even beyond 1 (runaway). The sheer probability of Aβ being close to 1 is astronomically small, never mind that that can make them simulate a tiny fragment of the climate history. Moreover, we would have observed quite different climate phenomena in the past.
For negative feedback, however, Aβ<0, the system is stable. Any deviation from a stable situation would have 'forces' bringing the system back to the stable situation. And this must be the case. All the time the climate system is brought off-balance by: seasonal (summer and winter) fluctuations, daily (day and night) fluctuations, random (weather) fluctuations, incidental (volcanic) events. The climate always recovers.
It is impossible to have large positive feedback (Aβ>1). It is highly unlikely to have positive feedback at all (Aβ>0). It is very likely there is negative feedback (Aβ<0).
This means that the resulting amplitude, y = A/(1-Aβ) x, is smaller than what can be expected without feedback, because A/(1-Aβ) < A. We can thus expect a climate sensitivity of CO2 smaller than 0.1 degrees for doubling CO2 in the atmosphere. The exact value can be a point of discussion.
For more information, contact me at The University of The Algarve,
Prof. Peter Stallinga
http://w3.ualg.pt/~pjotr