No, we do not have a
political agenda. We are a non-profit science organization! This research
gets funding from nobody!
|
Climate vs. weather and event
statistics
It is common knowledge that
climate and weather are two different things. Yet, very often the two
are confused, especially in the general public. Actually, the biggest
climate research is done by MetOffice, that is, the meteorological office in the UK.
This is dubious. |
|
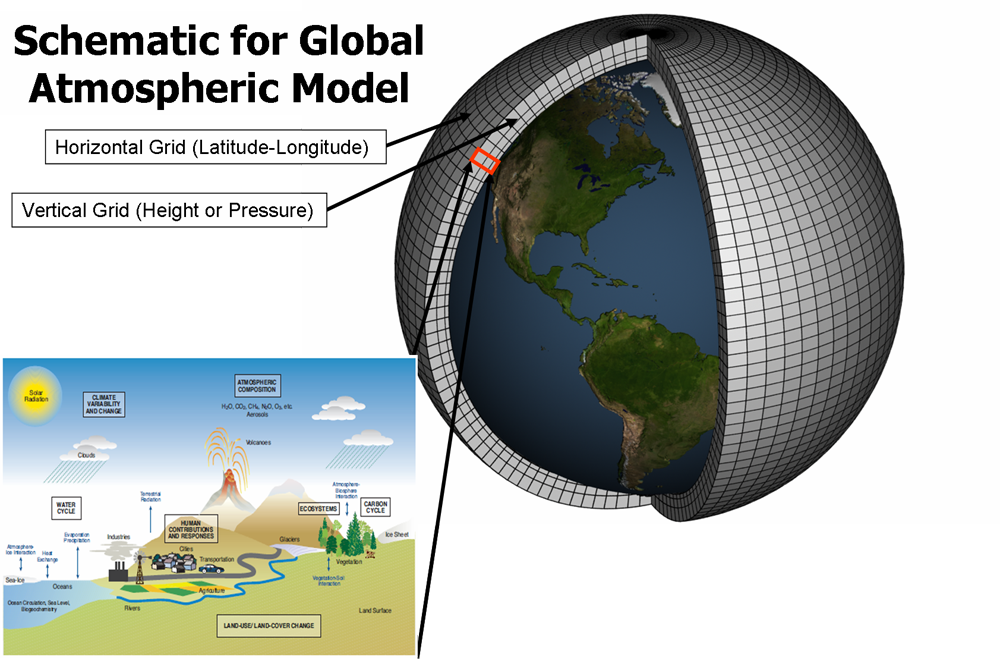
Finite-elements computer simulations
Think about it. The meteorologists use supercomputers to predict the weather. The atmosphere is an extremely difficult system, but for the meteorologists this is not a hindrance, because they just divide the atmosphere in 'tiny' cells in so-called finite-elements calculations. With some basic knowledge of atmospheric processes, they put everything in parameters.
http://www.simundo.org/science/simulation-grids/
The values of the parameters are then found in an iterative way:
- Predict the weather.
- See what the actual weather will be.
- Go back to the simulation and determine what values of parameters would have predicted the weather.
- Use these values for the next prediction iteration. Etc.
After thousands of iterations, a 'model' (simulation package) with reasonable predictive power (3-5 days) was achieved. The first predictions were abominable, but they kept on increasing the quality in the past 30 years.
An iteration takes about the same time span as the prediction (3 days; weather). It took about 4000 iterations to get it (reasonably) right.
If we use the same technique for the climate, we can expect the same convergence speed of getting the prediction right. The first predictions completely failed, as was to be expected (see IPCC predictions
 ) and we
can only hope to get a reasonable predictive quality after some
thousands of iterations. With each iteration taking about the time span
as the prediction (30 years; climate), we will have to wait hundreds of
centuries before we can predict the climate!
) and we
can only hope to get a reasonable predictive quality after some
thousands of iterations. With each iteration taking about the time span
as the prediction (30 years; climate), we will have to wait hundreds of
centuries before we can predict the climate!Another approach the meteorologists might have is to assume climate prediction is just long-term weather prediction. If we want to extend our weather prediction (days) to climate prediction (years), we are in for a long haul. Imagine, every day added to the weather prediction increases the difficulty by a factor of, say, 2 (which is an underestimation). Extending from 3 days to 30 years will increase the complexity by a factor 210000, which is approximately a factor 103000. Hold your horses building the new supercomputer!
The conclusion is that the meteorological approach, treating climate with weather tools, leads nowhere.
Statistics of weather extremes
Although it is generally accepted that climate is not weather and no weather event can be used as an indication for climate changes (be they man-made or not), lately, 'scientists', respond to the cry of the public to say something about the extreme weather events. "Are they, or are they not caused by climate changes?!" The response of these 'scientists' is to redefine science itself:

A citation from Peterson, et al. [1], which finishes with a mis-citation of a Nature article [2]. Actually, the referred article of Nature does not mention that "attribution statements ... are possible ...", but only that the public would like to hear such statements from scientists. There is a market for them (and this gives Peterson and coworkers a raison d'être). Let's analyze their reasoning which is representative for the modern culture in climate research.
Peterson and coworkers jump to the occasion in this paper "Explaining extreme events of 2011 from a climate perspective". They come with statements such as: "It cannot be excluded that the severe event X is caused by Global Warming" (quote is fictitious, just an example of what they might say). Meaning that, with 0.0000006%, it is likely to be caused and explained only by Global Warming. For Peterson and coworkers this is good enough. They can make statements about the cause of extreme weather events, as long as they provide a probability to the hypotheses, even if the probabilities calculated are insanely meaningless. The public happily ignores the probabilities and remain with the idea that "Extreme event X probably caused by Global Warming". And if, by this method, even for most of the weather extremes still nothing at all can be concluded(*), that doesn't matter; as long as there is sporadically one that escapes -- which is completely natural in any random-driven statistics; Statistically, no individual has any chance of winning the lottery, yet it happens every week -- these ones will make it to the headlines. Nobody will make it to the headlines saying
"A spell of extremely normal
weather hits Western Europe!!"
while scientifically it is just as interesting as the weather extremes.
(*) actually, if they did their work well, all could have been used, as shown later
Statistics, a tricky tool
Statistics are a very nice but dangerously complicated and tricky instrument. Let me give you an example:
 We roll a 6-face
die. Imagine we roll it 1000 times and find the statistics. They are
more-or-less as expected, with maybe a couple of times more a '3'
compared to a '5', etc. Lets assume that actually the die was
completely normal and had normal statistics with 1/6 probability for
each number. We roll a 6-face
die. Imagine we roll it 1000 times and find the statistics. They are
more-or-less as expected, with maybe a couple of times more a '3'
compared to a '5', etc. Lets assume that actually the die was
completely normal and had normal statistics with 1/6 probability for
each number.Now we roll it again, 3 times, and find '1', '6' and '4'. Have the probabilities of the die changed?! Absolutely! If we only look at the last rolls, '6' and '4', we can say that the probabilities for these rolls have changed from (average) 1/6, 1/6, 1/6, 1/6, 1/6, 1/6 to (the last single rolls) 0, 0, 0, 0, 0, 1 and 0, 0, 0, 1, 0, 0 as proven by the statistics. Well, it happened, duh! Whatever the laws of nature underlying it, the final outcome was '4', so the best model is the one that predicts (retroactively) a '4'. The real model, had we had knowledge of all underlying physics, would have predicted the above outcome. Continuing with 1/6-for-all probabilities just shows our ignorance of the physical laws of the system. But, without knowing why the outcome was '4', the probabilities must have been 100% for a '4', because that is what happened. The same with the weather. In other words, the weather events, like die-roll events, are completely deterministic. We are only blinded by our own ignorance into thinking there are some kind of probabilities involved. Like this, we are doomed to make wrong statements about the statistics. We can also reason the other way around (as modern climatologists do). While for the past the probabilities are 0% and 100%, and we know them now, what about the future? While for future events the probabilities are also 0% and 100%, the difference is we do not know them (yet). But we can use 'human' probabilities and predictions. That is, not probabilities, but a distribution of frequency of occurrence (which is for instance the climate or the bias of a die) whose distribution function we can estimate on basis of samples. (The term 'human probabilities' is used because humans see them as probabilities). Did this distribution function -- these 'human probabilities' for future events -- change? We can test the null-hypothesis 'nothing has changed' by asking "Not knowing anything about the system, what is the probability that the frequency-of-occurrence distribution is unaltered (for future die rolls), given the fact that the last roll was a '4'?" The answer might be 99.97%. The climate-alarmist-type scientists will then say "Probabilities have changed -- the die has changed -- with 0.03% probability". These statements are allowed "provided proper account is taken of the probabilistic nature of attribution", or in other words, as long as we supply an error margin with the statements. The media then pick it up "Die has changed!" and omit the ridiculous percentages which actually say that it is likely that nothing has changed. |
(Now apply this reasoning to the extreme weather events). Actually, any weather event is a sign/proof of climate changes!
Take this simplified imaginary situation: The only information we have is this: There was never a flooding in Pakistan. For the last 99 years (all measurements). Thus, the probability -- our best-estimator for the risk -- of flooding in Pakistan was 0%.
Then Pakistan gets hit by flooding. What is now our best-estimator of probability of flooding in the next year? 1%. Namely once every 100 years.
Conclusions:
1) The probability of flooding was 0% and the occurrence of flooding was 0% until last year.
2) The probability of flooding (and occurrence of flooding) last year was 100%.
3) The probability of flooding for the coming years is 1%.
Climate has changed! Sure it did. Our best-estimator has changed. And the more we start digging into the subject and the more we understand the physical laws governing the weather in Pakistan, the more we stop talking about probabilities and start talking about certainties: "It flooded because of X, Y and Z. These things were absent in the years before, and last year they were there. So, the system -- the climate -- has changed, namely in the aspects X, Y and Z"
Climate Alarmists would only be convinced of there not being climate changes if every year everywhere at every moment the weather is exactly the average. And, right they are; any deviation from average is considered (and in fact is) climate change.
The funny truth is that, if the weather has changed, so has the climate! It seems counter-intuitive, against what we learn at school, but it isn't. Climate is by definition the average weather of 30 years. If the weather is not exactly equal to the average of the last 30 years, this average, i.e. 'the climate', has changed, albeit it not with the same magnitude as the weather, since variations are amortized by a factor 30. (More precisely, in a 30-year-window moving-averaging definition of climate, the latest weather -- the weather that moves into the window -- should be equal to the weather exactly 30 years ago -- the weather that moved out of the window --, to result in unchanged climate). In other words, we can mix statements of weather and climate at will. Weather changes are climate changes, the difference between them is only an amortization factor of 30.
The question can now be answered: Was weather extreme X caused by climate changes? Absolutely! Any weather event (not only extremes) that did not happen before (at the same place and time of the year) is the result of climate changes, because the weather is completely deterministic, even if we, ignorami, cannot determine the underlying laws: There must have been changes in circumstances in the atmosphere (the climate) that caused a change of probability of occurrence of the weather event from 0% to 100% (Note that other probabilities do not exist in a deterministic world).
And if next year the event X does not occur, it means the weather/climate has changed again, from 100% back to 0% probability. And if we average the weather event occurrences over 30 years, we can say that the climate has changed if not exactly the same things happen at the same time.
And if we study more, namely the underlying physical processes, we can even determine what it is exactly that has changed in the climate. But that the climate has changed is irrefutable.
Moreover, since the climate from a human point of view is described as best-estimators of weather/climate parameters (temperature, precipitation, etc.) and they are the averages of those parameters in our averaging window, any weather event that has a value for a particular parameter that is not exactly equal to the average value will change the average and thus our best-estimator for that parameter and thus our estimation of the climate. "Did the climate change?" is thus converted into nothing more than "Has the average value changed?" The only discussion we can now have is about the direction and magnitude of changes and eventually about the permanent state of these changes, where the latter cannot be decided on statistics alone.
Conclusion: If we want to attribute a weather event to climate changes, we can fully justifiably do so. There is no problem with limitations of statistics. Any event can be used. For higher (emotional) impact, it is best to use weather catastrophes, though. Peterson et al. use these weather extremes and determine which ones had damages caused by the extremity of the weather itself (and thus undeniably the result of climate changes, i.e., Global Warming) and which ones occurred in 'normal' weather, but where the large catastrophic damages were caused by changes in society (removal of forests, excessive building in dangerous zones, etc.). Nothing more. Yet, the message to the public is "some weather extremes (that were catastrophic) were caused by Global Warming".
Weather events (extremes)
What
most modern climatologists often hint at is something like "The
(extreme) event X this year falls outside the statistics distribution
of all the other years (and this should be seen as a sign of climate
changes)". Imagine every year it rained between 1000 and 1100 mm and
suddenly there is 1200 mm of rainfall. These are obviously climate
changes, but, once again, it would also be climate changes if it had
rained 'abnormally' 1037 mm, since this has also never happened before.
Once again: any weather event is a sign of climate changes.
Moreover, either there is a trend (slowly rising from 1000 mm to 1100 mm to 1200 mm), or the 1200 mm is incidental, a one-time occurrence. While, trend or no trend they are climate changes, the attention is given only because of the surprising sudden step. Actually, the common opinion among scientists is that climate changes are more associated to gradual changes, things that are changing slowly and statistically proven by a large number of events. That makes isolated weather events useless for proving climate changes. So what that there is suddenly a flood in Thailand? The biggest ever? Big deal! Climate changes are changing trends and not incidents. Atypical events are normally considered 'outliers' and removed from the statistics. This is common practice. Only trends count. Of course they are signs of climate changes, but so is everything.
These outliers have only recently been included into the story, because of the public demand and the ease of selling the messages. This is easy money. (Catastrophe + climate change = money). Peterson and coworkers jump to the occasion.
The idea is that some weather parameter (like temperature or rainfall) is normally-distributed in a Gaussian probability function, exp(-(x-μ)2/σ2). If an event then lies more than 2σ away from the median μ, it is considered abnormal and thus a sign of climate changes. This is a misconception. This particular reasoning is false (although any event is a sign of climate changes, also outliers, as discussed above).
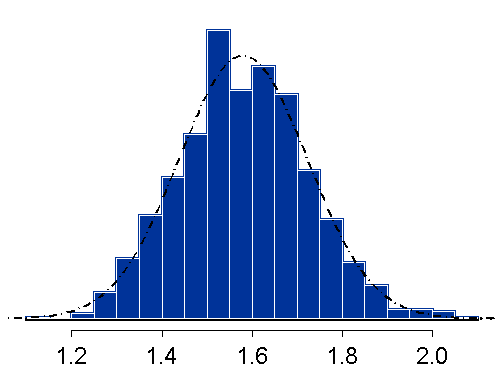
1) Assume the events are normally distributed with a Gaussian function exp(-(x-μ)2/σ2)
2) Find the parameters μ and σ of the real data
3) Determine by a Student's-t test if a new event lies within 2σ or not and if it supports the null-hypothesis or is an extreme event
The reasoning goes wrong with the basic assumption, the distribution is namely not Gaussian. Upon arrival of a new datapoint that is falling outside the expected range of the normal distribution, it is then concluded that the parameter μ has changed (climate changes), but it might as well be that the conclusion should be that your assumption of normal distribution is wrong.
Most events (like earthquakes and volcano eruptions, etc.) follow a power law, meaning that an event with magnitude x has x-α frequency of occurrence, with α a constant. See the work of Newman for an excellent summary of these power-law functions[3]. Power-law functions can mimic Gaussian functions, especially for small numbers of samples, but they lack the parameter σ and drawing conclusions on basis of this parameter can thus not be done. Actually, these functions are horrendously difficult to work with. It is as good as impossible to draw conclusions with these functions, as anybody working with them knows. In some cases also stretched-exponential functions are found, exp(-xβ), equally messy. And even if it is not a power-law or stretched-exponential distribution function, that does not mean that the distribution is as simple as normal Gaussian. Just because you cannot come up with something better does not make your choice valid. The outliers prove you wrong.
Larger events, outliers, have tiny probability, but they will happen every now and then. Imagine that a Pakistan-scale flooding has a yearly probability of 0.1% of occurring in Pakistan. (Once every 1000 years on average). Negligible! Has never happened, obviously. Can be ignored. But every now and then it will happen, against all odds. And since there are many 'Pakistans' in the world, the probability that it happens somewhere in the world is very large.
This is again similar to the probability of winning the lottery. Winning it has so immensely tiny probability that we can safely neglect the possibility this ever happening to us. Yet, it happens every week to someone, because there are many people playing the lottery. (The winner normally attributes it to divine intervention because of its low probability).
It would be very very unlikely indeed if nowhere in the world some exceptionally unlikely weather-event would happen. Looking backwards, afterwards we can then say "This event was extremely improbable and is (thus) a sign of climate changes". The word 'thus' is imagined by the public or inserted by journalists somewhere in the process (no self-respecting scientist will say it). The second part -- 'climate changes' -- is an empty statement, since, as discussed above, anything is a sign of climate changes. What remains is "The event had small occurrence before" (but occurred now, it is an outlier).
The conclusion is that no extreme event ('outlier') can be considered a proof of climate changes as such (even though any event is a sign of climate changes) regardless of the fact that it lies far outside the normal distribution.
This is the reason why normally outliers are thrown away. They are messing up everything. Yet, they come in handy for the panic-hungry Climate Alarmists. They are easily sold as 'something out of the ordinary' (thus the public opinion is that they must be global warming), something destructive and easily statistically proved to be caused by climate changes.
[1] T.C. Peterson, et al., Am. Meteo. Soc. July 2012, p.1041 (2012).
[2] Nature v.477, p.131 (2011).
[3] M.E.J. Newman, Contemp. Phys. v.46, p.323 (2005).
For more information, contact me at The University of The Algarve,
Prof. Peter Stallinga
http://w3.ualg.pt/~pjotr